8  Intercept

This chapter evaluates the intercept of the growth, survival, and recruitment models. We use trait information extracted from the literature to compare the average estimation for each demographic model. The traits of growth classes, maximum observed size, maximum observed age, and shade tolerance are extracted from Burns, Honkala, et al. (1990), while the seed mass comes from Dı́az et al. (2022).

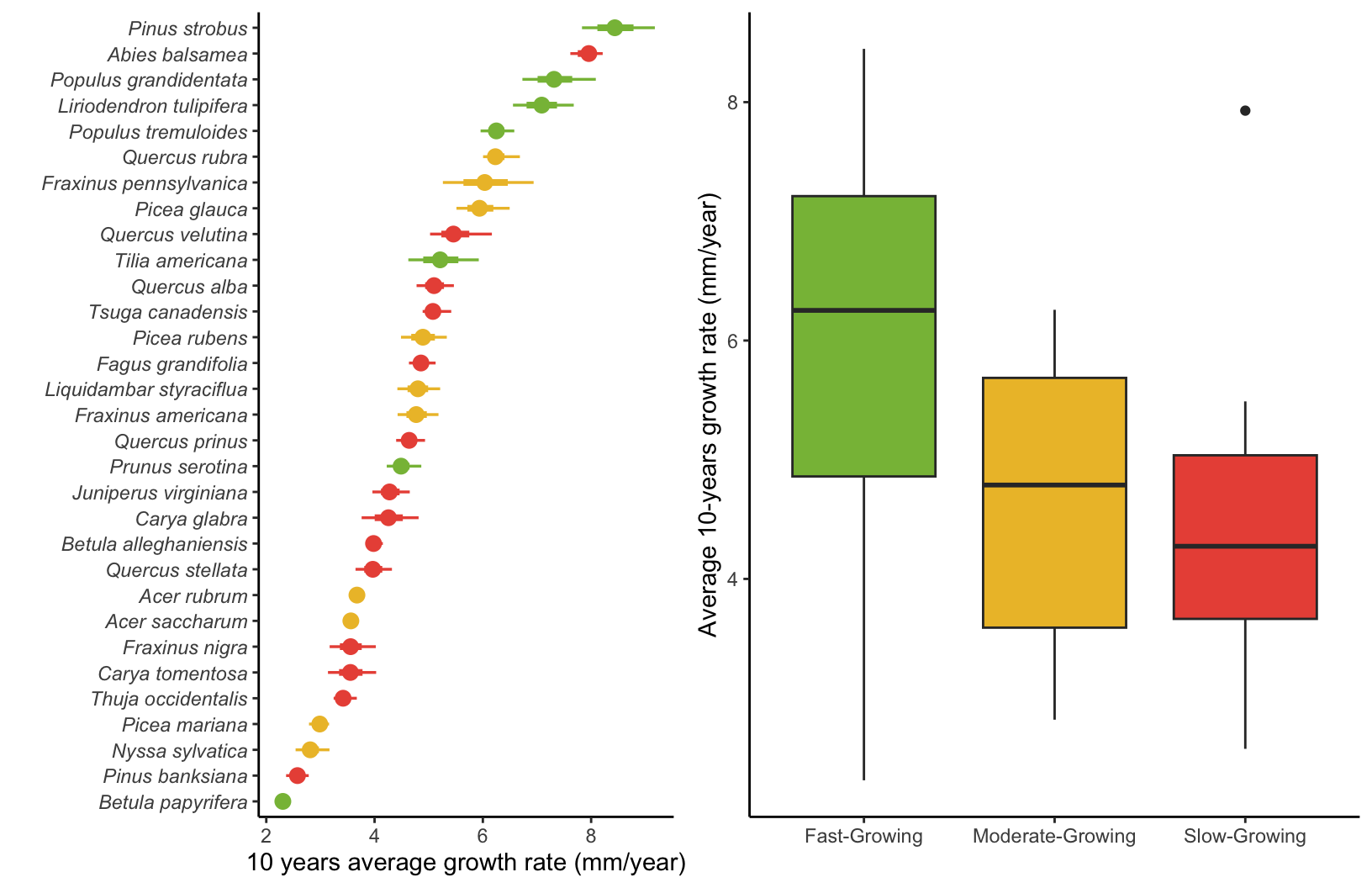
Growth rate

Because the growth rate intercept decreases non-linearly with size and is governed by the interaction of two parameters (\(\Gamma\) and \(\zeta_{\infty}\)), we computed the average growth rate over a 10-year interval. Also, because the size of the individual is integrated into the Von Bertalanffy growth model, we computed the 10-year growth average starting from the lower size threshold of 12.7 cm, where growth is optimal.

Figure 8.1: Intercept of the growth model using the 10-year average growth rate. Species are classified by their general growth trait following Burns, Honkala, et al. (1990)

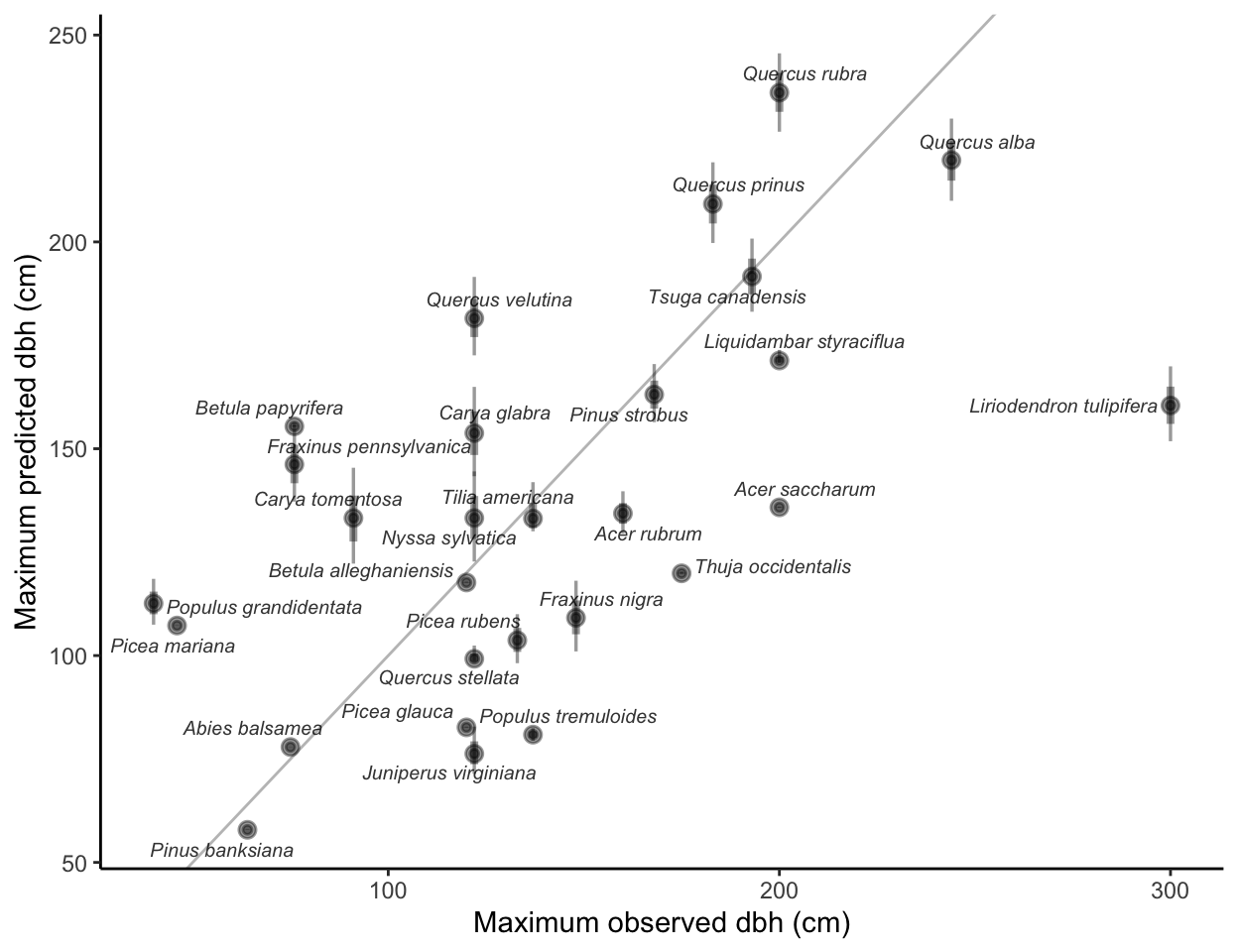
The following figure compares the maximum observed size in the literature with the asymptotic size (\(\zeta_{\infty}\)), denoting the size where the growth rate converges to zero.

Figure 8.2: Correlation between maximum observed size in literature following Burns, Honkala, et al. (1990) and estimated parameter \(\zeta_{\infty}\)

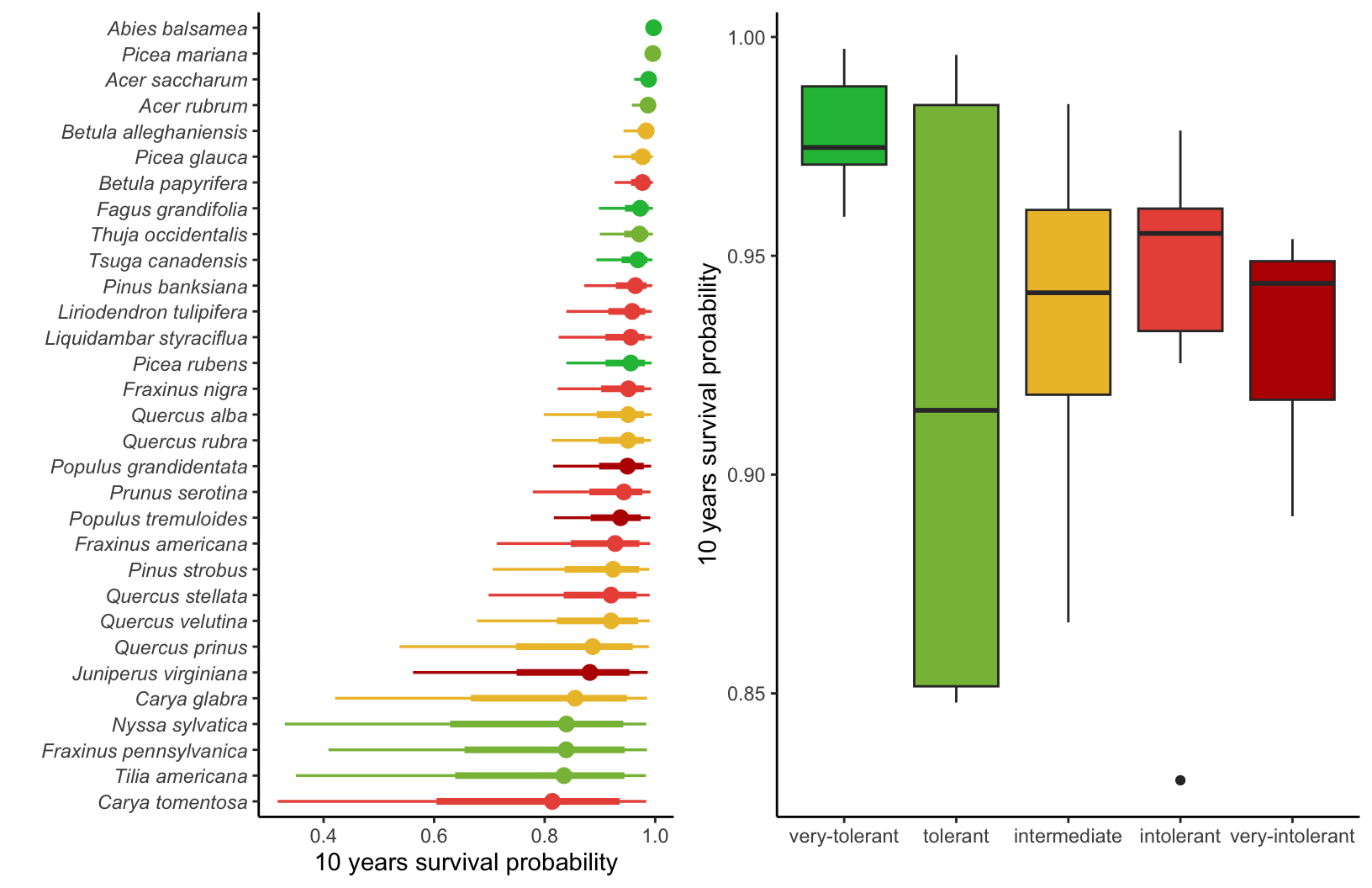
Mortality probability

Similar to the growth rate, the survival model has a temporal component in which survival probability (\(\psi\)) decreases exponentially with time. So, we computed the 10-year average mortality probability as the intercept for the survival model.

Figure 8.3: Intercept of the survival model using a 10-year mortality probability. Species are classified by their shade tolerance trait following Burns, Honkala, et al. (1990)

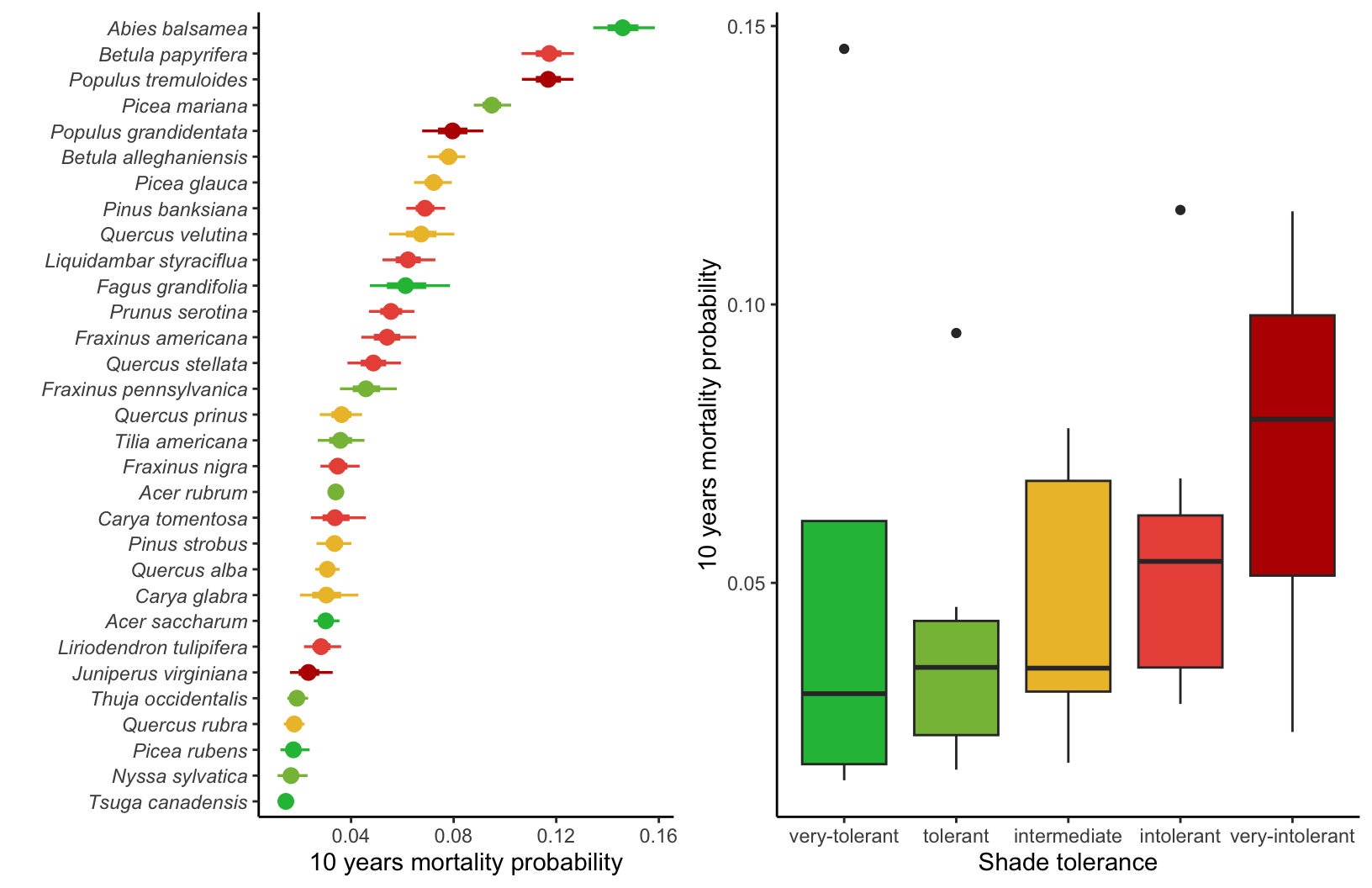
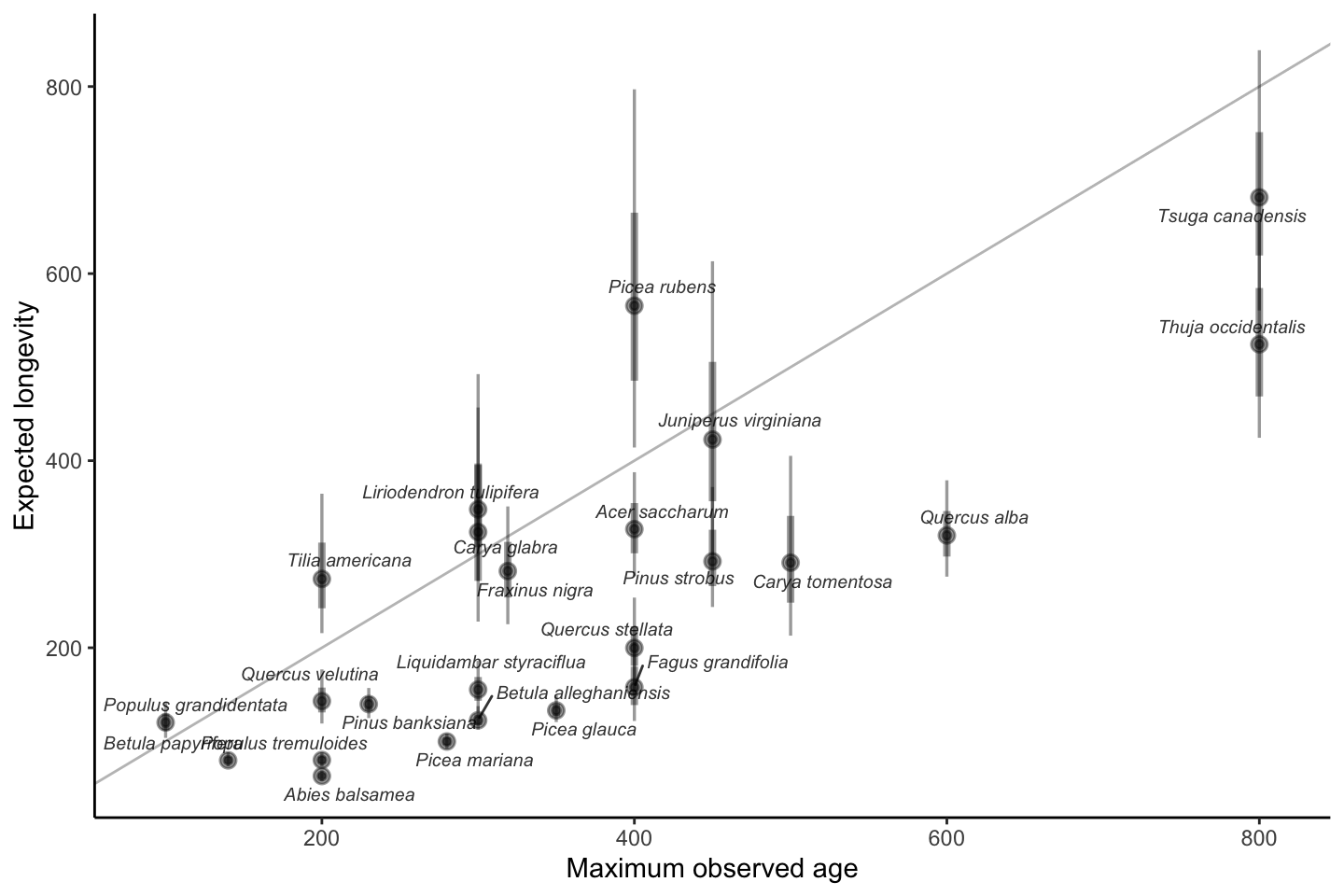
Alternatively, we can also use the parameter \(\psi\) to derive the expected longevity (\(L\)), which can be determined as \(L = e^{\psi}\). The Figure 8.4 correlated the maximum size observed in the literature (Burns, Honkala, et al. 1990) with longevity (\(L\)).

Figure 8.4: Correlation between maximum size observed in the literature (Burns, Honkala, et al. 1990) and the predicted longevity posterior distribution.

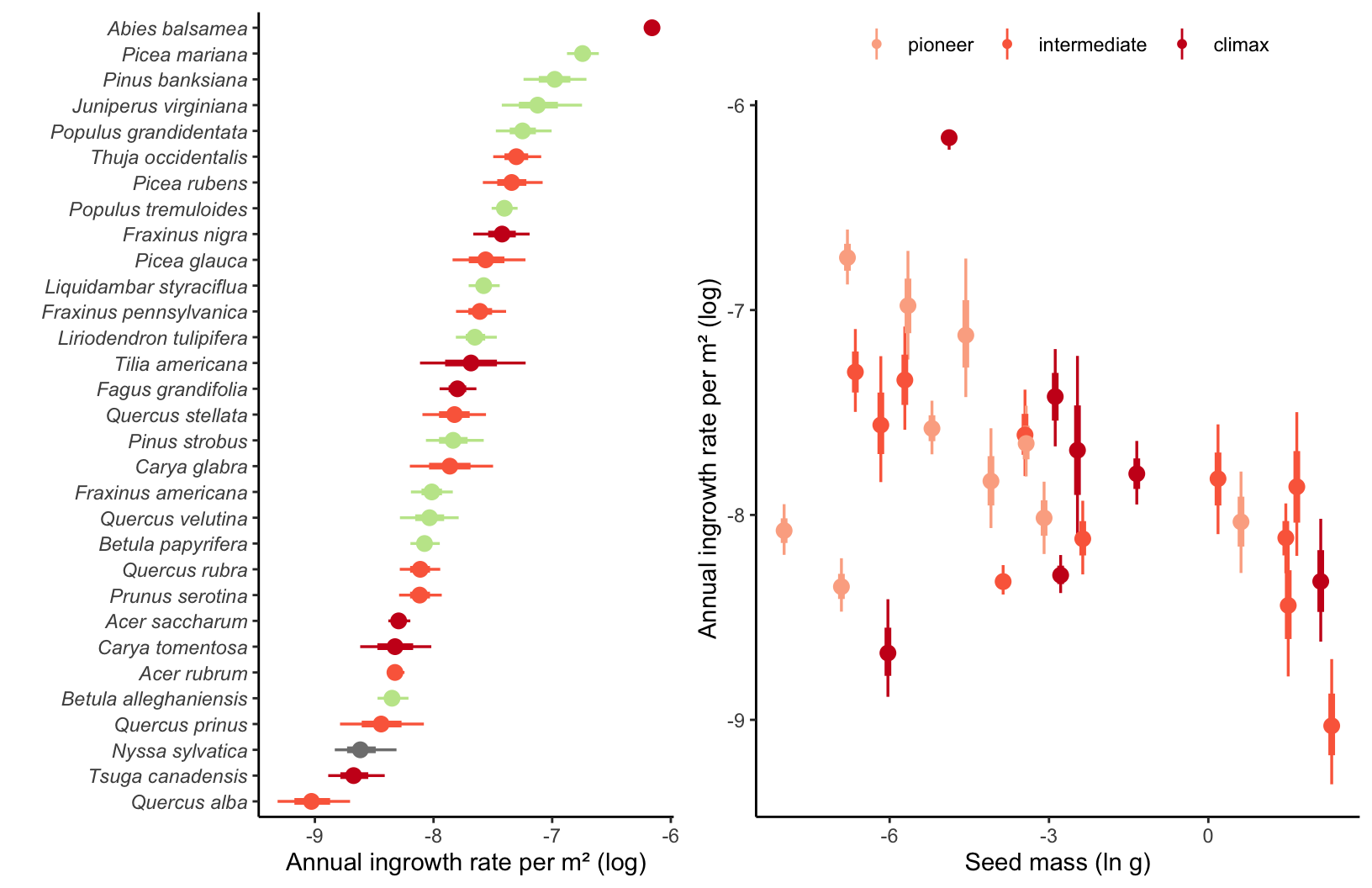
Ingrowth rate

The ingrowth model comprises two intercept components: the annual ingrowth rate per square meter (\(\phi\)) and the annual survival probability \(\rho\). In the context of the survival submodel for the ingrowth rate, we computed the 10-year survival probability of ingrowth individuals just like in the survival model.

Figure 8.5: Intercept of the ingrwoth model for the number of individuals that ingress the population per year per m\(^2\). Species are classified by their successional status following Burns, Honkala, et al. (1990).

Figure 8.6: Intercept of the annual survival probability for the ingrowth model. Species are classified by their shade tolerance trait following Burns, Honkala, et al. (1990).

Burns, Russell M, Barbara H Honkala, et al. 1990. “Silvics of North America: 1. Conifers; 2. Hardwoods Agriculture Handbook 654.” US Department of Agriculture, Forest Service, Washington, DC.

Dı́az, Sandra, Jens Kattge, Johannes HC Cornelissen, Ian J Wright, Sandra Lavorel, Stéphane Dray, Björn Reu, et al. 2022. “The Global Spectrum of Plant Form and Function: Enhanced Species-Level Trait Dataset.” Scientific Data 9 (1): 755.