suppressPackageStartupMessages(library(tidyverse))
baseURL <- 'https://raw.githubusercontent.com/willvieira/forest-IPM/master/R/'
# source the three R scripts with the IPM functions
c('vital_rates.R', 'kernel.R', 'BasalArea_competition.R') |>
walk(~source(paste0(baseURL, .x)))15 A guide to use the forest-IPM code
The forest-IPM code is available in this GitHub repository: https://github.com/willvieira/forest-IPM. This repository contains a collection of R functions designed for implementing the vital rates and Kernel functions and the necessary data parameters for the 31 fitted species. Below, I will briefly overview how to load and execute these functions and outline the results you can expect from the model.
Before we begin, we need to access the set of parameters for each species-demographic model. As described in Chapter 7, the parameters are stored in an ownCloud folder, which you can access through this link: Parameter Dataset. Once you have downloaded the parameters, you need to specify the path location where the parameters are stored. To do this, create a file named _data.path and place it at the root of your project.
Loading the functions and parameters
We start by sourcing the IPM-specific functions directly from GitHub:
The first wrapper function is the getPars_sp(), which loads species-specific parameters. The sp and path arguments define the species based on their ID, as outlined in Table 2.1, and specify the location path where these parameters are stored. The method argument allows you to specify whether you wish to load the mean value or a random draw from the posterior distribution for each parameter. The model argument defines which specific model you want to download the parameters. However, the IPM functions are currently available only for the complete model, so this argument should remain intcpt_plot_comp_clim.
pars_abibal <- getPars_sp(
sp = '18032ABIBAL',
method = 'mean', # `mean` or `random`
model = 'intcpt_plot_comp_clim',
path = file.path(readLines('_data.path'), 'output_sim_processed')
)The pars_abibal object is a simple list for each vital rate with named vectors representing the parameters associated with that particular vital rate.
(pars_abibal)$growth
Beta Lmax optimal_prec optimal_temp r sigma_obs
-0.04082927 778.92148600 0.67333923 0.47041774 -4.34529798 7.95712862
sigma_plot tau_prec tau_temp theta
0.47382333 2.71067700 13.12657955 0.52418479
$mort
Beta optimal_prec optimal_temp psi sigma_plot tau_prec
-0.008103519 0.677269861 0.452655943 4.141692735 1.070949032 4.753038180
tau_temp theta
1.364021618 0.021797255
$rec
beta_p mPop_log optimal_BA optimal_prec optimal_temp p_log
0.005473664 -6.097612710 22.210854250 0.675963964 0.464676533 -8.209122925
sigma_BA sigma_plot tau_prec tau_temp
46.503604600 1.066220577 8.270941957 12.747742450
$sizeIngrowth
phi_time sigma_size size_int
3.57045138 49.59714057 0.03174647 Defining model conditions
Let us establish the initial community structure based on the size of individuals. Populations are characterized by density functions that describe the distribution of individuals across the size range covered by the IPM (\([L, U]\)). In this context, we set the lower threshold of the size distribution (\(L\)) to 127 mm in dbh, following the FIA protocol. As the von Bertalanffy growth model incorporates a parameter that determines the size at which the growth rate converges to zero (\(\zeta_{\infty}\)), we define the upper boundary of the size distribution to be the species-specific \(\zeta_{\infty}\). The h argument specifies the bin size in millimeters for the discretized kernel, while N represents the total population size, defined as \(\int_L^{\zeta_{\infty}} n(z) \mathrm{d}z\). Given that this approach generates distributions randomly, the accuracy threshold determines the acceptance of the brute force approximation of the integral to match the expected population size N. Finally, the meanSize and sdSize are the parameters in the natural scale of the lognormal distribution used to generate random size distribution.
N_sp <- init_pop(
params = pars_abibal,
L = 127,
h = 1,
N = 10,
accuracy = 0.001,
meanSize = 130,
sdSize = 1.8
)The N_sp object is also a list composed of the (i) species-specific mesh points (needed internally to build the kernel), the density function describing the distribution of individuals, and the h bin size.
Code
N_sp |>
enframe() |>
filter(name == 'Nvec') |>
unnest(value) |>
mutate(x = 127:(n() + 126)) |>
ggplot(aes(x, value)) +
geom_point(alpha = 0.5) +
geom_path() +
theme_minimal() +
labs(
x = 'Size (mm)',
y = 'Density'
) 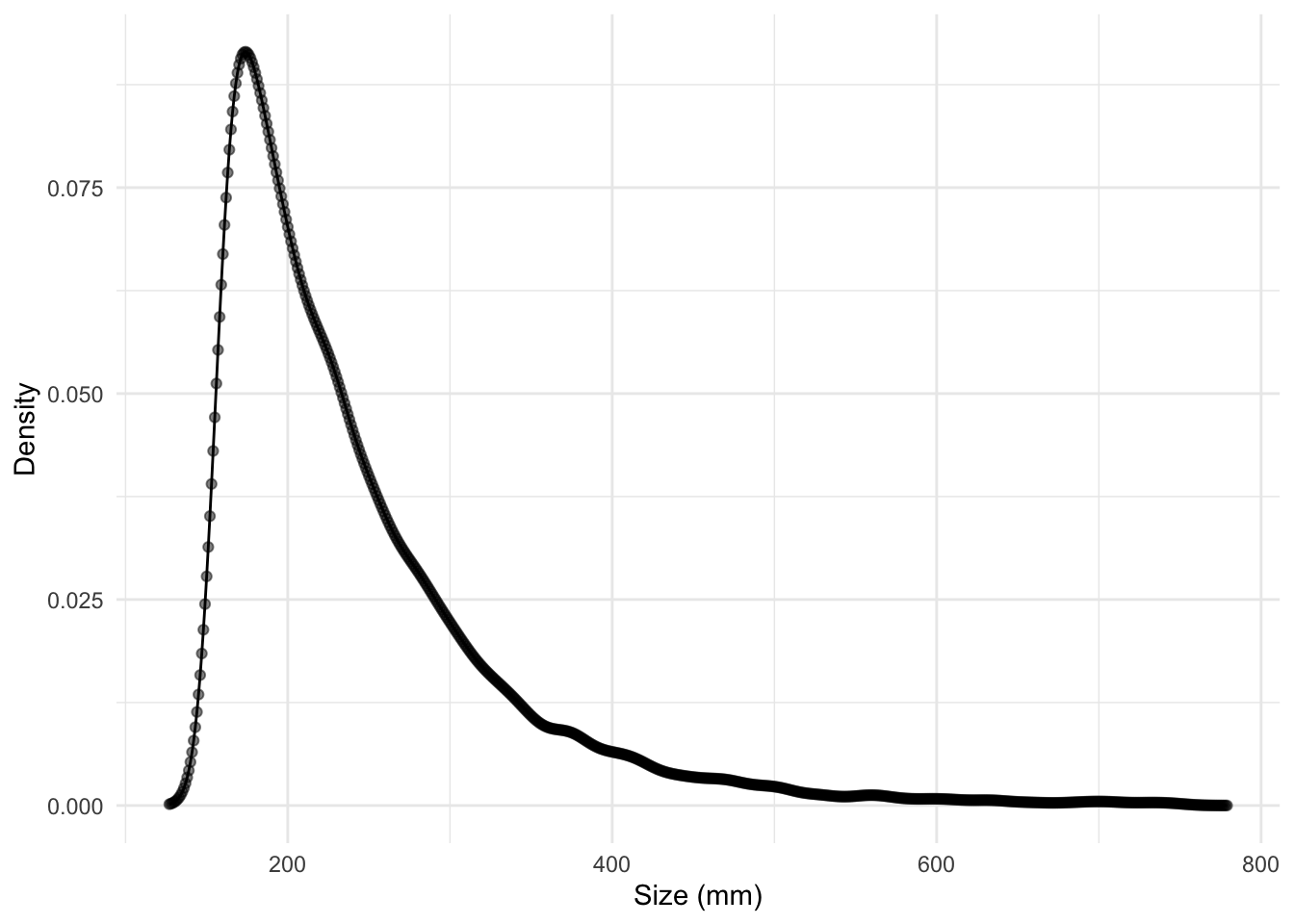
N_sp$Nvec object. The dots are the discretized bin values.Additionally, we need to create a second structured population vector for the heterospecific species. This vector will represent the size distribution of all species other than the focal species and will be used to compute the heterospecific competition effect.
While we could use the init_pop() function as described above, with similar parameters except for the N, which can take any desired value, we will introduce a second approach. This alternative method allows us to approximate a continuous population vector based on observed dbh measurements. Given that we already have an object from the init_pop() function, we need to feed the dbh_to_sizeDist() function with the observed dbh values and the output of the init_pop() function as follows:
# generate random observed values of dbh
obs_dbh <- runif(2, 127, 500)
# create a continuous population vector based on observed dbh measurements
N_het <- dbh_to_sizeDist(
dbh = obs_dbh,
N_intra = N_sp
)The final condition parameters necessary to run the IPM model are:
delta_time = 1 # the time interval from $t$ to $t+1$. Usually set to 1.
plotSize = 200 # plot size in squared meters
Temp = 0.3 # mean annual temperature scaled between 0 and 1
Prec = 0.8 # mean annual precipitation scaled between 0 and 1
plot_random = rep(0, 3) # plot random effects for c(growth, survival, and recruitment)Run the IPM
The primary function of the forest IPM is the mkKernel().
K_abibal = mkKernel(
Nvec_intra = N_sp,
Nvec_inter = N_het,
delta_time = delta_time,
plotSize = plotSize,
Temp = Temp,
Prec = Prec,
pars = pars_abibal,
plot_random = plot_random
)The K_abibal object is a list of the \(P\), \(F\), and \(K\) matrices of dimension \(z^2\) as described in Equation 14.2. This kernel object is the core output of the IPM model, serving as the foundation for projecting populations over time or calculating the asymptotic population growth rate (\(\lambda\)) and other metrics.
We can extract the asymptotic population growth rate (\(\lambda\)) using the leading eigen value of the matrix \(k\):
(max(Re(eigen(K_abibal$K)$values)))[1] 1.209816Given that our matrix is density-dependent, we can project the population vector over time by continuously updating the Kernel at each time step to account for the evolving size distribution of individuals. In the following code, we demonstrate a simple loop to trace the evolving population over time while assuming that there is only conspecific density-dependence (N_het = 0). Note that this code is slow and can take 5-10 minutes to run due to the slow eigen() computation.
set.seed(0.0)
# Initial population size (small)
N_sp <- init_pop(
params = pars_abibal,
L = 127,
h = 1,
N = 1
)
# define no heterospecific competition
N_het <- init_pop(
params = pars_abibal,
L = 127,
h = 1,
N = 0
)
# generate initial Kernel
K0 = mkKernel(
Nvec_intra = N_sp,
Nvec_inter = N_het,
delta_time = delta_time,
plotSize = plotSize,
Temp = Temp,
Prec = Prec,
pars = pars_abibal,
plot_random = plot_random
)
time_max = 200
# vector to save lambda over time
lambdas = max(Re(eigen(K0$K)$values))
# matrix to save size distribution
ntmat = matrix(0, nrow = length(N_sp$Nvec), ncol = time_max)
ntmat[, 1] <- N_sp$Nvec
for(Time in 2:time_max)
{
# update the state
ntmat[, Time] <- K0$K %*% ntmat[, Time - 1]
N_sp$Nvec <- ntmat[, Time]
# update the kernel
K0 <- mkKernel(
Nvec_intra = N_sp,
Nvec_inter = N_het,
delta_time = delta_time,
plotSize = plotSize,
Temp = Temp,
Prec = Prec,
pars = pars_abibal,
plot_random = plot_random
)
# calculate pop growth rate
lambdas[Time] = max(Re(eigen(K0$K)$values))
cat(' Time step', Time, 'of', time_max, '(', round(Time/time_max * 100, 1), '%)\r')
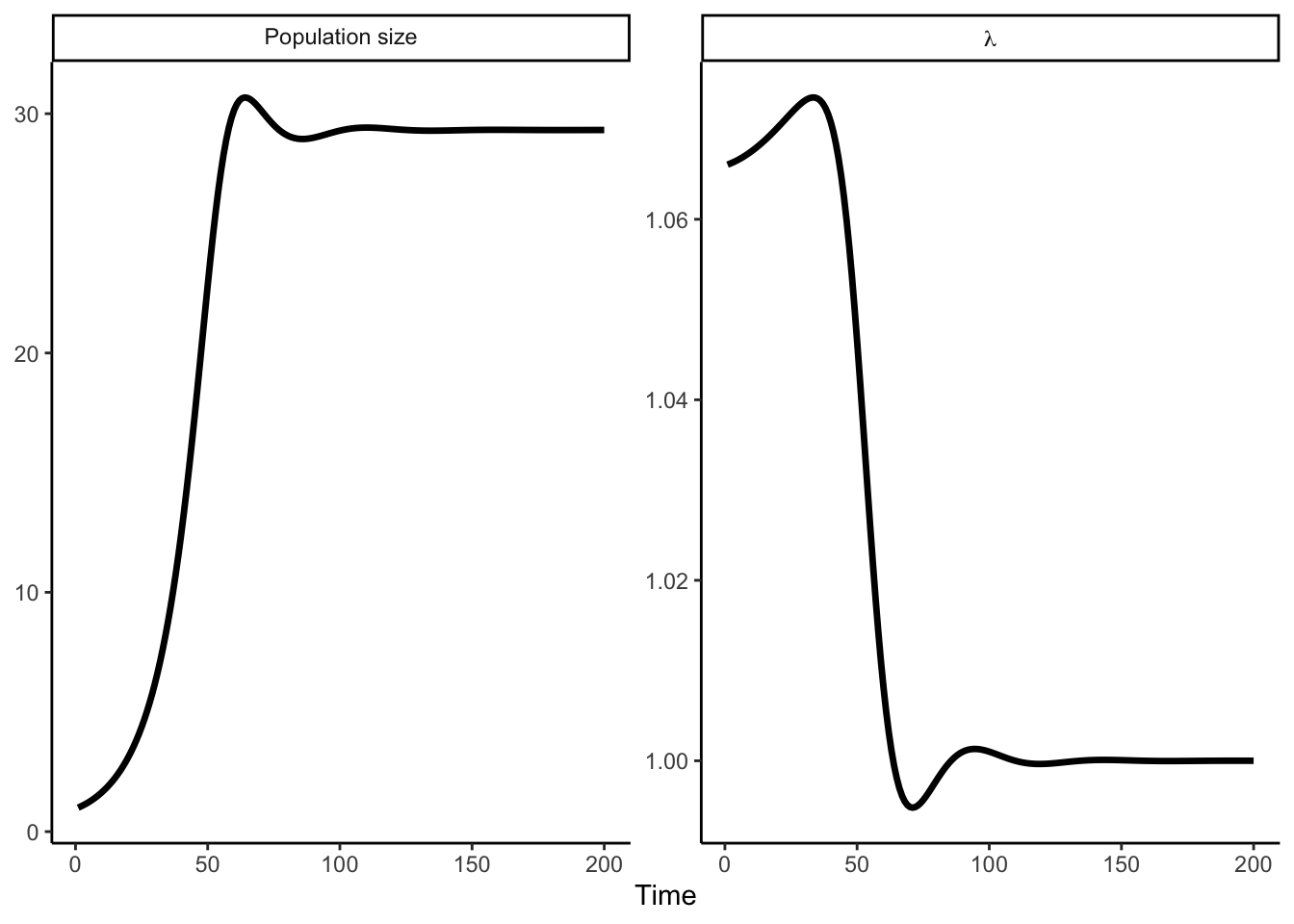
}For each time iteration, we saved the focal species’ size (\(z\)) distribution and the population growth rate (\(\lambda\)). We can visualize how each measure involved time for these species-specific conditions. In Figure 15.2 and Figure 15.3, we can visualize how \(\lambda\) and the size density distribution evolve.
Code
ntmat |>
as_tibble() |>
pivot_longer(cols = everything(), values_to = 'Density') |>
mutate(Time = parse_number(name)) |>
group_by(Time) |>
reframe(N = sum(Density)) |>
left_join(
lambdas |>
enframe(name = 'Time') |>
rename(lambda = value)
) |>
pivot_longer(cols = c(N, lambda)) |>
mutate(
name = factor(name, levels = c('N', 'lambda'), labels = c(expression(textstyle('Population size')), expression(lambda)))
) |>
ggplot() +
aes(Time, value) +
facet_wrap(
~name,
scales = 'free_y',
labeller = label_parsed
) +
geom_path(linewidth = 1.2) +
theme_classic() +
labs(
y = NULL
)
Code
suppressPackageStartupMessages(library(plotly))
ntmat |>
as.data.frame() |>
pivot_longer(cols = everything(), values_to = 'Density') |>
mutate(Time = parse_number(name)) |>
group_by(Time) |>
mutate(x = 127:(n() + 126)) |>
ggplot() +
aes(x, Density) +
aes(group = name) +
aes(frame = Time) +
geom_path() +
theme_classic() +
xlab('Size (mm)') ->
p
ggplotly(p) |>
animation_opts(frame = 50) |>
animation_slider(
hide = FALSE,
currentvalue = list(prefix = "Time step: ", font = list(color = 'black'))
) |>
animation_button(
x = 0.9, xanchor = 'left', y = 1, yanchor = 'top'
)